Descarga e instalación de RStudio y R en un equipo con Windows 11. Tipos de datos en R, operadores relacionales, lógicos, de asignación, aritméticos. Diferentes tipos de objetos: vectores/arrays, listas, matrices, factores y data frames.
- Descargar e instalar RStudio y R en Windows.
- Tipos de datos básicos en R.
- Operadores aritméticos en R (suma, resta, multiplicación, módulo, raíz cuadrada).
- Operadores lógicos en R.
- Operadores relacionales en R.
- Operadores de asignación en R.
- Vectores/Arrays en R.
- Listas (Lists) en R.
- Matrices (matrix) en R.
- Factores (Factor) en R.
- Data Frames en R.
Descargar e instalar RStudio y R en Windows
Accederemos a la web oficial de RStudio y descargaremos la versión Free (que es suficiente para la gran parte de tareas). En nuestro caso descargaremos el fichero RStudio-2022.02.3-492.exe correspondiente a la versión Free para Windows 10 y 11.
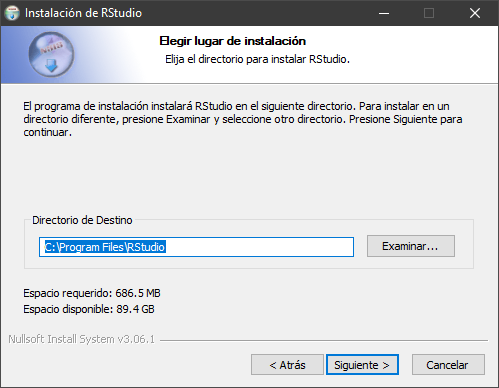
La instalación de RStudio es bastante sencilla, indicamos la ruta de instalación:
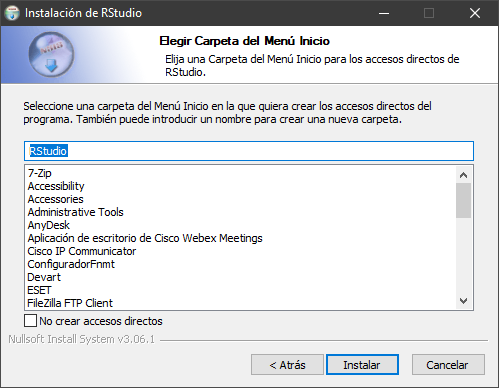
Y poco más:
La primera vez que abrimos RStudio nos preguntará cómo queremos instalar R y qué versión. Por defecto detectará la arquitectura del sistema operativo y nos propondrá la versión R para la misma, en nuestro caso «R64», por lo que marcaremos «Use your machine’s default version of R64 (64-bit)». Para el motor de renderización, dejaremos la opción «Auto-detect (recommended)» en «Rendering Engine»:

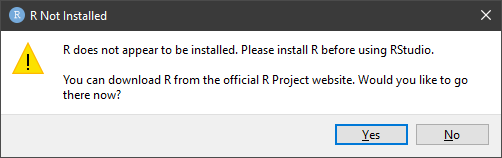
Puesto que R no está instalado aún, nos mostrará un mensaje para acceder a la web de descarga de R, responderemos «Yes»:
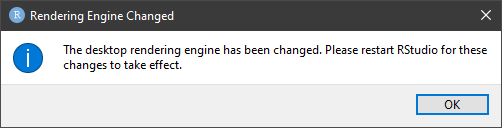
Nos indicará el motor de renderización cargado. Pulsaremos «OK»:
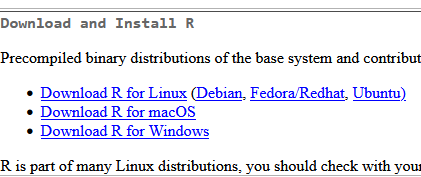
Descargaremos el instalador de R, en la actualidad la versión 4.2.1:

Descargaremos el instalador para Windows, desde el origen que queramos, por ejemplo desde:
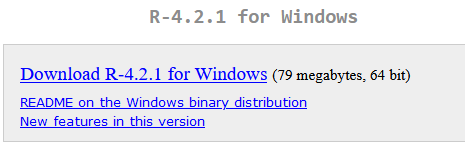
Descargaremos la versión de R para nuestro sistema operativo:
Descargaremos el paquete «base»:
Download R-4.2.1 for Windows
Instalaremos R for Windows 4.2.1, la instalación es bastante sencilla también:
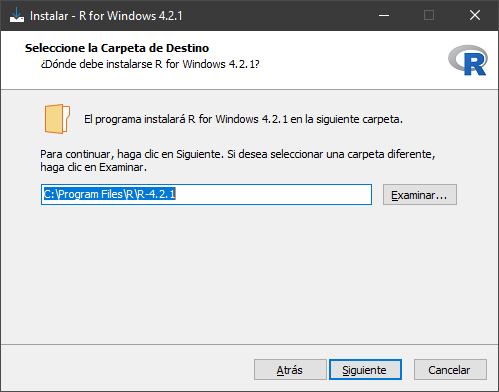
Marcaremos «Main Files», «64-bit Files» y «Message translations»:
Indicaremos el modo de visualización, MDI, aunque el entorno de R no lo usaremos, usaremos RStudio:

Marcaremos «Ayuda HTML»:
Y finalizaremos la instalación de R for Windows 4.2.1:

Para algunos paquetes puede que necesitemos Rtools, que podremos descargar desde:
https://cran.rstudio.com/bin/windows/Rtools/rtools42/rtools.html
Tipos de datos básicos en R
R incluye los siguientes tipos de datos «atómicos» (básicos):
| Tipo | Descripción | Ejemplo asignación |
| Numeric | Números decimales | importe <- 2500.55 print(class(importe)) Devolverá: «numeric» |
| Logical | Operaciones lógicas | ejecutar <- TRUE print(class(ejecutar)) Devolverá: «logical» |
| Character | Cadenas de texto | mensaje <- «Estamos trabajando en R» print(class(mensaje)) Devolverá: «character» |
| Complex | Números complejos | numComplejo <- 3+2i print(class(numComplejo)) Devolverá: «complex» |
| Integer | Números enteros | edad <- 34L print(class(edad)) Devolverá: «integer» |
| Raw | Para la cadena de texto: «Estamos trabajando en R desde ProyectoA», la conversión a tipo Raw con charToRaw, devolverá: 45 73 74 61 6d 6f 73 20 74 72 61 62 61 6a 61 6e 64 6f 20 65 6e 20 52 20 64 65 73 64 65 20 50 72 6f 79 65 63 74 6f 41 | tipoRaw <- charToRaw(«Estamos trabajando en R desde ProyectoA») print(class(tipoRaw)) Devolverá: «raw» |
Operadores aritméticos en R (suma, resta, multiplicación, módulo, raíz cuadrada)
Como casi cualquier lenguaje, R cuenta con todas las operaciones básicas posibles: suma, resta, multiplicación, división, módulo, funciones matemáticas (raíz cuadrada, potencia, trigonométricas, …):
| Operador aritmético | Descripción operación |
|---|---|
| + | Suma |
| – | Resta |
| * | Multiplicación |
| / | División |
| ^ | Exponencial |
| ** | Exponencial |
| %% | Módulo |
| %/% | División entera |
| %*% | Multiplicación matricial |
| %o% | Producto exterior |
| %x% | Producto Kronecker |
Ejemplo de uso en código R:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
miSuma <- (34 + 6) print(miSuma) [1] 40 miResta <- miSuma - 21 print(miResta) [1] 19 miProducto <- (miSuma * 4) print(miProducto) [1] 160 miModulo <- 20 %% 4 print(miModulo) [1] 0 miRaiz <- sqrt(25) print(miRaiz) [1] 5 miPotencia <- 5^4 print(miPotencia) [1] 625 miSeno <- sin(90) print(miSeno) [1] 0.8939967 miCoseno <- cos(90) print(miCoseno) [1] -0.4480736 |
Operadores lógicos en R
Los operadores lógicos en R:
| Operador lógico | Descripción operación |
|---|---|
| & | Comparación lógica AND (Y) |
| && | Comparación lógica AND (Y) entre vectores |
| | | Comparación lógica OR (O) |
| || | Comparación lógica OR entre vectores |
| ! | Negación lógica NOT (NO) |
| xor() | Exclusión OR, equivalente a !( x | y) |
Operadores relacionales en R
Los operadores relacionales en R:
| Operador relacional | Descripción operación |
|---|---|
| > | Mayor que |
| < | Menor que |
| >= | Mayor o igual que |
| <= | Menor o igual que |
| == | Igual a |
| != | Distinto a |
Operadores de asignación en R
Los operadores de asignación en R:
| Operador de asignación | Descripción del operador |
|---|---|
| <- | Asignación izquierda |
| -> | Asignación derecha |
| <<- | Asignación lexicográfica izquierda |
| ->> | Asignación lexicográfica derecha |
Vectores/Arrays en R
R admite, como es lógico, vectores (arrays). A continuación algunos ejemplos de asignación y operaciones (concatenar, combinar, …). Los vectores se establecen con c() y pueden contener elementos de los tipos de datos atómicos anteriores.
Para crear una variable que contiene un vector con números (numeric) y mostrar sus valores, usaremos:
|
1 2 |
vectorNumeros <- c(10,20,30,40,50,12.55,50.43) print(vectorNumeros) |
Podremos unir vectores, y generar nuevos vectores concatenados:
|
1 2 3 4 |
vectorNumeros <- c(10,20,30,40,50,12.55,50.43) vectorNumeros2 <- c(4,5,6) vectorNumeros3 <- c(vectorNumeros,450.89,37,vectorNumeros2) print(vectorNumeros3) |
Nos devolverá:
10.00 20.00 30.00 40.00 50.00 12.55 50.43 450.89 37.00 4.00 5.00 6.00
Podremos realizar operaciones con estos vectores, como por ejemplo calcular la raíz cuadrada de todos sus elementos:
|
1 2 |
vectorRaizN3 <- sqrt(vectorNumeros3) print(vectorRaizN3) |
Nos devolverá:
3.162278 4.472136 5.477226 6.324555 7.071068 3.542598 7.101408 21.234171 6.082763 2.000000 2.236068 2.449490
Podremos ordenar elementos de un vector, mostrando la posición por índice de cada elemento ordenado, usaremos order:
|
1 2 |
vectorNumerosOrdenado <- order(vectorNumeros) print(vectorNumerosOrdenado) |
En este caso en vectorNumerosOrdenado mostrará la posición de cada elemento en el orden que le corresponde, para el vector:
10.00 20.00 30.00 40.00 50.00 12.55 50.43
Devolverá:
1 6 2 3 4 5 7
El elemento 6 del vector pasa a la posición 2 según su valor y orden.
Para ordenar un vector mostrando sus valores ordenados usaremos sort:
|
1 2 |
vectorNumerosOrdenado <- sort(vectorNumeros) print(vectorNumerosOrdenado) |
Devolverá:
10.00 12.55 20.00 30.00 40.00 50.00 50.43
También podemos usar la función anterior order, estableciendo el índice de salida del vector, obtendremos el mismo resultado que con sort:
|
1 |
vectorNumerosOrdenado <- vectorNumeros[order(vectorNumeros)] |
Para establecer el orden descendente usaremos:
|
1 |
vectorNumerosOrdenado <- sort(vectorNumeros, decreasing = TRUE) |
Podremos añadir elementos a un vector existente con append. Por ejemplo, para añadir el valor 999 al primer elemento del vector vectorNumeros:
|
1 2 |
vectorNumeros <- append(vectorNumeros,999,0) print(vectorNumeros) |
Devolverá:
999.00 10.00 20.00 30.00 40.00 50.00 12.55 50.43
También podremos eliminar elementos de un vector. Por ejemplo, para eliminar los elementos 20.00 y 30.00, usaremos su posición en el vector (la 3ª y la 4ª):
|
1 |
vectorNumeros <- vectorNumeros[-c(3,4)] |
Quedando:
999.00 10.00 40.00 50.00 12.55 50.43
Por supuesto podremos obtener el tamaño de un vector (número de elementos) con length:
|
1 |
length(vectorNumeros) |
Crear un vector desde una secuencia:
|
1 2 3 |
vectorSerieNumeros <- c(12:8) print(vectorSerieNumeros) [1] 12 11 10 9 8 |
Saber si un elemento existe en un vector (membresía):
|
1 2 3 4 5 6 |
print(vectorSerieNumeros) [1] 12 11 10 9 8 5 %in% vectorSerieNumeros [1] FALSE 8 %in% vectorSerieNumeros [1] TRUE |
Por supuesto, se puede realizar cualquier operación básica como obtener el valor de un índice del vector, añadir y eliminar elementos, unir vectores y cualquier otra acción.
Listas (Lists) en R
R permite crear listas de elementos heterogéneos (de tipos de datos diferentes). Por ejemplo, para crear una lista con un vector, textos y números:
|
1 2 3 |
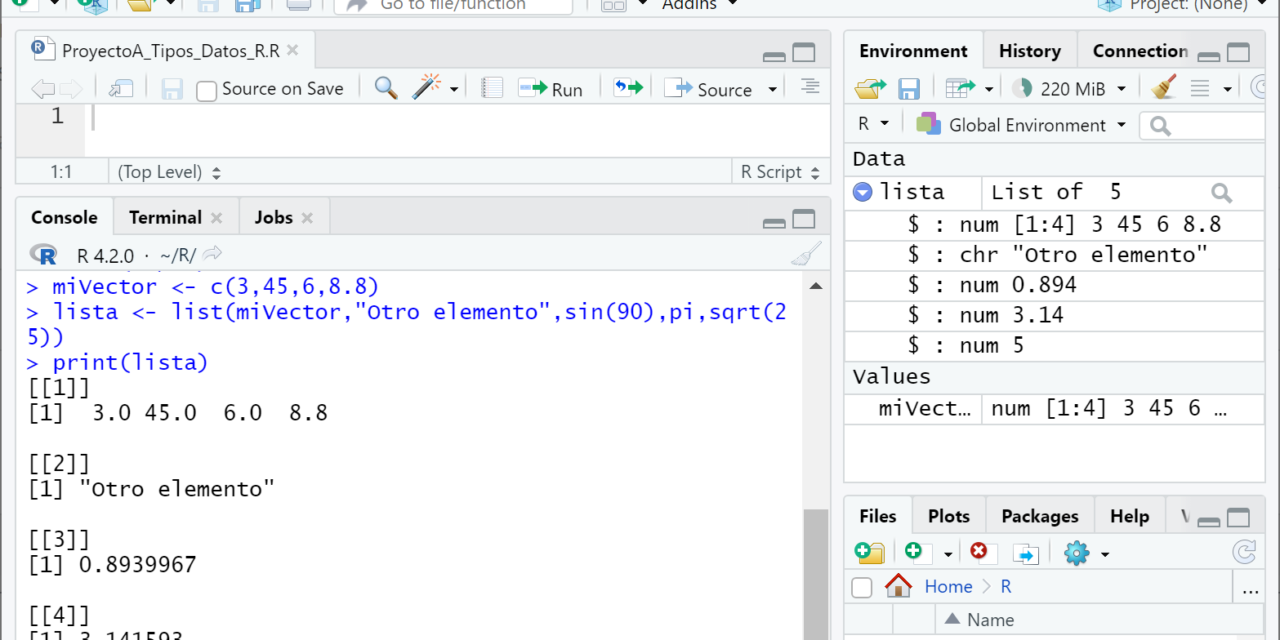
miVector <- c(3,45,6,8.8) lista <- list(miVector,"Otro elemento",sin(90),pi,sqrt(25)) print(lista) |
Hemos creado una lista con un array, un texto, el cálculo de la función sin(90), el número pi y el cálculo de la función sqrt(25). Devolverá:
|
1 2 3 4 5 6 7 8 9 10 |
[[1]] [1] 3.0 45.0 6.0 8.8 [[2]] [1] "Otro elemento" [[3]] [1] 0.8939967 [[4]] [1] 3.141593 [[5]] [1] 5 |
Por supuesto, se puede realizar cualquier operación básica como obtener el valor de un índice de la lista, añadir y eliminar elementos, unir listas y cualquier otra acción. Por ejemplo, para unir dos listas:
|
1 2 3 4 5 |
miVector <- c(3,45,6,8.8) lista <- list(miVector,"Otro elemento",sin(90),pi,sqrt(25)) lista2 <- list("Uno","Dos","Tres") listasUnidas <- c(lista,lista2) print(listasUnidas) |
Devolverá los valores de la variable listasUnidas:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
[[1]] [1] 3.0 45.0 6.0 8.8 [[2]] [1] "Otro elemento" [[3]] [1] 0.8939967 [[4]] [1] 3.141593 [[5]] [1] 5 [[6]] [1] "Uno" [[7]] [1] "Dos" [[8]] [1] "Tres" |
Para modificar el valor de un elemento de una lista. Por ejemplo, para modificar el elemento 6 de la lista listasUnidas al valor «Elemento cambiado»:
|
1 |
listasUnidas[6] <- "Elemento cambiado" |
Se puede convertir una lista en vector (siempre que los elementos de la lista sean del mismo tipo, si no lo son, los convertirá a texto (character)). Por ejemplo, si convertimos la lista anterior que contiene números, texto y vectores a vector, convertirá todos sus elementos a texto (character):
|
1 |
vectorConvertido <- unlist(listasUnidas) |
Devolverá:
|
1 2 3 4 |
[1] "3" "45" "6" [4] "8.8" "Otro elemento" "0.893996663600558" [7] "3.14159265358979" "5" "Elemento cambiado" [10] "Dos" |
Si convertimos una lista de números a vector, sí que respetará el tipo de datos numérico:
|
1 2 |
listaNumeros <- list(1,4,55,6.6,12.5,67667.4) vectorConvertidoNumeros <- unlist(listaNumeros) |
Devolverá:
|
1 |
[1] 1.0 4.0 55.0 6.6 12.5 67667.4 |
Para eliminar un elemento de la lista, por ejemplo el elemento de la posición 4, usaremos:
|
1 |
listasUnidas[4] <- NULL |
Para mostrar el valor de un elemento de la lista, usaremos:
|
1 |
print(listasUnidas[4]) |
Podemos nombrar los elementos de una lista. Por ejemplo, si tenemos la lista:
|
1 2 3 |
lsDireccionesIP <- list("192.168.10.100","192.168.10.150","192.168.10.45",c(45,32,125)) names(lsDireccionesIP) <- c("IP1","IP2","IP3","Visitas") print(lsDireccionesIP) |
Devolverá:
|
1 2 3 4 5 6 7 8 |
$IP1 [1] "192.168.10.100" $IP2 [1] "192.168.10.150" $IP3 [1] "192.168.10.45" $Visitas [1] 45 32 125 |
Por supuesto, podremos tener listas de listas:
|
1 2 3 4 |
lista1 <- list(1,4,5,6,23) lista2 <- list(pi,sin(32),"Lista 2 texto") lista3 <- list(lista1,lista2,"Otro valor más") print(lista3) |
Devolverá:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
[[1]] [[1]][[1]] [1] 1 [[1]][[2]] [1] 4 [[1]][[3]] [1] 5 [[1]][[4]] [1] 6 [[1]][[5]] [1] 23 [[2]] [[2]][[1]] [1] 3.141593 [[2]][[2]] [1] 0.5514267 [[2]][[3]] [1] "Lista 2 texto" [[3]] [1] "Otro valor más" |
Matrices (matrix) en R
Para crear una matriz usaremos:
|
1 2 |
matriz1 <- matrix( c('Alonso','Juan','Pepe','Vicente',46,37,39,65)) print(matriz1) |
Al no haber indicado las filas y columnas, creará una matriz unidimensional:
|
1 2 3 4 5 6 7 8 9 |
[,1] [1,] "Alonso" [2,] "Juan" [3,] "Pepe" [4,] "Vicente" [5,] "46" [6,] "37" [7,] "39" [8,] "65" |
Si redefinimos la matriz anterior indicando 2 filas y 4 columnas con:
|
1 |
matriz1 <- matrix( matriz1, nrow = 2, ncol = 4, byrow = TRUE) |
Ahora sí nos habrá creado una matriz de 2×4 (dos filas y cuatro columnas:
|
1 2 3 |
[,1] [,2] [,3] [,4] [1,] "Alonso" "Juan" "Pepe" "Vicente" [2,] "46" "37" "39" "65" |
Podremos hacer múltiples operaciones con matrices: sumar, restar, multiplicar, trasponer, determinante, inversa, rango, dimensión, etc.
Por ejemplo, para sumar dos matrices (mostramos su dimensión con dim):
|
1 2 3 4 5 6 7 8 9 10 11 |
m1 <- matrix(c(2, 6, 5.5, 8), ncol = 2, byrow = TRUE) m2 <- matrix(c(12, 3.3, 2, 3.5), ncol = 2, byrow = TRUE) dim(m1) [1] 2 2 dim(m2) [1] 2 2 mSuma <- m1+m2 print(mSuma) [,1] [,2] [1,] 14.0 9.3 [2,] 7.5 11.5 |
Para trasponer una matriz (columnas por filas y filas por columnas):
|
1 2 3 4 5 6 7 |
mTraspuesta <- t(matriz1) print(mTraspuesta) [,1] [,2] [1,] "Alonso" "46" [2,] "Juan" "37" [3,] "Pepe" "39" [4,] "Vicente" "65" |
Para multiplicar una matriz por un escalar:
|
1 2 3 4 5 6 7 8 9 |
print (mSuma) [,1] [,2] [1,] 14.0 9.3 [2,] 7.5 11.5 mEscalar <- mSuma * 8 print(mEscalar) [,1] [,2] [1,] 112 74.4 [2,] 60 92.0 |
Para multiplicar dos matrices (el número de columnas de la primera matriz debe ser igual al número de filas de la segunda):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
print(m1) [,1] [,2] [1,] 2.0 6 [2,] 5.5 8 print(m2) [,1] [,2] [1,] 12 3.3 [2,] 2 3.5 mMultiplicacion <- m1%*%m2 print(mMultiplicacion) [,1] [,2] [1,] 36 27.60 [2,] 82 46.15 |
El determinante de una matriz:
|
1 2 3 4 5 6 |
print(m1) [,1] [,2] [1,] 2.0 6 [2,] 5.5 8 det(m1) [1] -17 |

Aplicar operación por filas, por ejemplo, sumar las filas de una matriz (devolverá una matriz de una fila y tantas columnas como tuviera la matriz a sumar, en cada columna devolverá el resultado de la operación, sumando todas las columnas de esa fila):
|
1 2 3 4 5 6 7 8 9 |
m2 <- matrix(1:12, nrow= 4, ncol = 3) print(m2) [,1] [,2] [,3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 apply(m2, 1, sum) [1] 15 18 21 24 |
Multiplicar las columnas de una matriz ( (devolverá una matriz de una fila y tantas columnas como tuviera la matriz a multiplicar, en cada columna devolverá el resultado de la operación, multiplicando todas las columnas de esa fila):
|
1 2 |
apply(m2, 2, prod) [1] 24 1680 11880 |
Otras operaciones:
- Inversa de una matriz: solve(m1,m2).
- Diagonal de una matriz: diag(m1).
Factores (Factor) en R
R permite las estructuras de datos factor, que son objetos que se crean utilizando un vector. Almacenan el vector junto con los distintos valores de los elementos del vector, como etiquetas. Las etiquetas son siempre de tipo carácter, independientemente de si se trata de caracteres, números o booleanos en el vector de entrada. Son útiles en el modelado estadístico.
Por ejemplo:
|
1 2 3 4 5 6 7 8 9 |
colores <- c("azul","verde","rojo","verde","verde","negro") print(colores) [1] "azul" "verde" "rojo" "verde" "verde" "negro" factorColores <- factor(colores) print(factorColores) [1] azul verde rojo verde verde negro Levels: azul negro rojo verde print(nlevels(factorColores)) [1] 4 |
Data Frames en R
Los Data Frames son objetos de datos tabulares. A diferencia de una matriz, cada columna puede contener diferentes tipos de datos. Es una lista de vectores de igual longitud.
|
1 2 3 4 5 6 7 8 9 10 11 |
dfDatosUsuarios <- data.frame( edad = c(32,45,18), sexo = c("hombre","mujer","mujer"), altura = c(172,160,168), peso = c(79,56,50.8) ) print(dfDatosUsuarios) edad sexo altura peso 1 32 hombre 172 79.0 2 45 mujer 160 56.0 3 18 mujer 168 50.8 |